신경망은 분류와 회귀 모두 사용할 수 있다. 하지만 어떤 문제냐에 따라 출력층에서 사용하는 활성화 함수가 달라진다. 일반적으로 회귀에는 항등 함수를, 분류에는 소프트맥스 함수를 사용한다.
| 머신러닝 문제는 분류(classification)와 회귀(regression)로 나뉜다. 분류는 데이터가 어느 클래스에 속하느냐는 문제이고, 회귀는 입력 데이터에서 (연속적인) 수치를 예측하는 문제이다. |
1. 항등 함수와 소프트맥스 함수 구현하기
항등 함수(identity function)는 입력을 그대로 출력한다. 그래서 출력층에서 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 된다. 항등 함수에 의한 변환은 은닉층에서의 활성화 함수와 마찬가지로 화살표로 그린다.


exp($x$)는 $e^x$ 을 뜻하는 지수 함수(exponential function)이다($e$는 자연상수). $n$은 출력층의 뉴런 수, $y_k$는 그 중 $k$번째 출력임을 뜻한다. 소프트맥스 함수의 분자는 입력 신호 $a_k$의 지수 함수, 분모는 모든 입력 신호의 지수 함수의 합으로 구성된다.
아래의 그림처럼 소프트맥스의 출력은 모든 입력 신호로부터 화살표를 받는다. 소프트맥스 함수 식의 분모에서 보듯, 출력층의 각 뉴런이 모든 입력 신호에서 영향을 받기 때문이다.
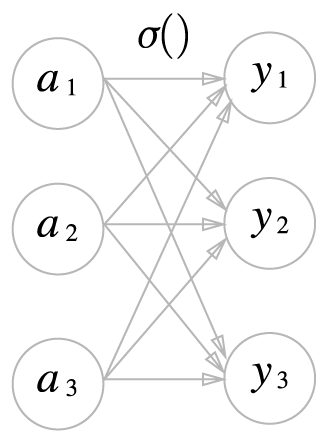
소프트맥스 함수의 구현
import numpy as np
a = np.array([0.3, 2.9, 4.0])
exp_a = np.exp(a) #지수함수
print(exp_a)
sum_exp_a = np.sum(exp_a) #지수함수의 합
print(sum_exp_a)
y = exp_a / sum_exp_a
print(y)[실행 결과]
[ 1.34985881 18.17414537 54.59815003]
74.1221542101633
[0.01821127 0.24519181 0.73659691]
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
2. 소프트맥스 함수 구현 시 주의점
소프트맥스 함수의 코드는 컴퓨터로 계산할 때 오버플로라는 문제를 일으킨다. 소프트맥스 함수는 지수 함수를 사용하는데, 지수함수는 쉽게 아주 큰 값을 출력한다. 이런 큰 값끼리 나눗셈을 하면 결과 수치가 불안정해진다.

위 식의 전개 과정을 살펴보면, 첫번째 변형에서 $C$라는 임의의 정수를 분자와 분모 양쪽에 곱했다(양쪽에 같은 수를 곱했으니 결국 똑같은 계산이다). 그리고 $C$를 지수함수 exp() 안으로 옮겨 $logC$로 만든다. 마지막으로 $logC$를 $C'$라는 새로운 기호로 바꾼다.
위 식이 말하는 것은 소프트맥스의 지수함수를 계산할 때 어떤 정수를 더하거나 빼도 결과는 바뀌지 않는다는 것이다. 여기서 $C'$에 어떤 값을 대입해도 상관없지만, 오버플로를 막을 목적으로는 입력 신호 중 최댓값을 이용하는 것이 일반적이다.
import numpy as np
a = np.array([1010, 1000, 990])
print(np.exp(a) / np.sum(np.exp(a))) #소프트맥스 함수의 계산, 제대로 계산되지 않는다.
c = np.max(a) #c=1010(최댓값)
print(a - c)
print(np.exp(a - c) / np.sum(np.exp(a - c)))[실행 결과]
[nan nan nan]
[ 0 -10 -20]
[9.99954600e-01 4.53978686e-05 2.06106005e-09]위 예를 보면 아무런 조치 없이 그냥 계산하면 nan이 출력된다. 하지만 입력 신호 중 최댓값(c)을 빼주면 올바르게 계산할 수 있다.
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) #오버플로 대책
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
3. 소프트맥스 함수의 특징
softmax() 함수를 사용하면 신경망의 출력은 다음과 같이 계산할 수 있다.
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
print(np.sum(y))[실행 결과]
[0.01821127 0.24519181 0.73659691]
1.0소프트맥스 함수의 출력은 0에서 1.0 사이의 실수이고, 출력의 총합은 1이다. 출력 총합이 1이 된다는 점은 소프트맥스 함수의 중요한 성질이며, 이 성질 덕분에 소프트맥스 함수의 출력을 확률로 해석할 수 있다.
위의 결과로 보자면, y[0]의 확률은 0.018, y[1]의 확률은 0.245, y[2]의 확률은 0.737로 해석할 수 있다.
여기서 주의할 점은, 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않는다. 이는 지수함수가 $y=exp(x)$가 단조 증가 함수이기 때문이다.
[참고] 단조 증가 함수란 정의역 원소 $a, b$가 $a \leq b$일 때, $f(a) \leq f(b)$ 가 성립하는 함수
실제로 앞의 예에서 $a$의 원소들 사이의 대소 관계가 $y$의 원소들 사이의 대소 관계로 그대로 이어진다.
신경망을 이용한 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식한다. 그리고 소프트맥스 함수를 적용해도 출력이 가장 큰 뉴런의 위치는 달라지지 않는다. 결과적으로 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 된다.
| 머신러닝의 문제 풀이는 학습과 추론(inference)의 두 단계를 거쳐 이뤄진다. 학습 단계에서 모델을 학습하고, 추론 단계에서 앞서 학습한 모델로 미지의 데이터에 대해서 추론(분류)을 수행한다. 위에서 설명한 대로, 추론 단계에서는 출력층의 소프트맥스 함수를 생략하는 것이 일반적이지만, 신경망을 학습시킬 때는 출력층에서 소프트맥스 함수를 사용한다. |
4. 출력층의 뉴런 수 정하기
출력층의 뉴런 수는 풀려는 문제에 맞게 적정히 정해야 한다. 분류에서는 분류하고 싶은 클래스 수로 설정하는 것이 일반적이다. 예를 들어 입력 이미지를 숫자 0부터 9 중 하나로 분류하는 문제라면 아래의 그림처럼 출력층의 뉴런을 10개로 설정한다.

뉴런의 회색 농도가 해당 뉴런의 출력 값의 크기를 의미하므로, 이 신경망이 선택한 클래스는 $y_2$, 입력 이미지를 숫자 '2'로 판단했음을 의미한다.
'Deep Learning 1 > 신경망' 카테고리의 다른 글
| 6. 손글씨 숫자 인식 (0) | 2020.04.27 |
|---|---|
| 4. 3층 신경망 구현하기 (0) | 2020.04.23 |
| 3. 다차원 배열의 계산 (0) | 2020.03.31 |
| 2. 활성화 함수 (0) | 2020.03.18 |
| 1. 퍼셉트론에서 신경망으로 (0) | 2020.02.12 |